- 量子力学、解析力学を既習であり、場の量子論を志す学部生(学部3〜4年前期程度)
- 物理学を専攻する大学院生・研究者(修士課程以上)
この記事では、場の量子論の前段階および場の解析力学の導入として「ネーターの定理」について解説します。
本記事を読むことで
対称性と保存則の感覚を大まかに掴んで頂けると幸いでございます。
本記事を執筆している、私トーマは、東京大学で物理学者として勤務しています。
そんな私が分かりやすく解説いたします。
なお過去の記事でも、場の理論・解析力学の導入に関して解説しております。
合わせてご覧いただけると幸いでございます。
復習:オイラー・ラグランジュ方程式
私の過去の記事
の内容をざっくりとおさらいします。
計算過程は上記の記事を参考にしてください。
スカラー場 \( \phi(x) \) に依存する作用 \( S \) は
\begin{eqnarray}
S \left( \phi \right) = \int d^{d} x \mathcal{L} (\phi, \partial_{\mu} \phi) \tag{1} \label{ac}
\end{eqnarray}
と書けます。
ここで \( \mathcal{L} (\phi, \partial_{\mu} \phi) \) はラグランジアン密度です。
この時、作用の微小変化 \( \delta S \) は
\begin{eqnarray}
\delta S = \int d^{d} x \left[ \frac{\partial \mathcal{L}}{\partial \phi} \delta \phi + \frac{\partial \mathcal{L}}{\partial \left( \partial_{\mu} \phi \right)} \delta \left( \partial_{\mu} \phi \right) \right] \tag{2} \label{dac}
\end{eqnarray}
と書けます。
作用の微小変化を0にする時、オイラー・ラグランジュ方程式
\begin{eqnarray}
\frac{\partial \mathcal{L}}{\partial \phi} \, – \, \partial_{\mu} \left( \frac{\partial \mathcal{L}}{\partial \left( \partial_{\mu} \phi \right)} \right) = 0 \tag{3} \label{eleq}
\end{eqnarray}
が導かれます。
場のカレント、保存量
場の変換 \( \phi (x) \rightarrow \phi^{\prime}(x) \) に対して、作用 \( S \) が不変に保たれる時、これを「(場の変換に対して)系に対称性がある」といいます。
以下では、無限小パラメータ \( \epsilon^{a} \) を用いて、場の無限小変換
\begin{eqnarray}
\phi (x) \rightarrow \phi^{\prime}(x) = \phi (x) + \epsilon^{a} G_{a} \left( \phi \right) \tag{4} \label{inftra}
\end{eqnarray}
を考えます。
ここで \( G_{a} \left( \phi \right) \) は、場の変換に関する生成子とします。
ネーターの定理
ネーターの定理とは
系に連続的な対称性がある場合には、その変換に対応する保存量が存在する。
と言うものです。
以下で、それを示したいと思います。
無限小変換(式 \eqref{inftra})の下で、作用の微小変化(式 \eqref{dac})を考えると
\begin{eqnarray}
\delta S &=& \int d^{d} x \left[ \frac{\partial \mathcal{L}}{\partial \phi} \epsilon^{a} G_{a} \left( \phi \right) + \frac{\partial \mathcal{L}}{\partial \left( \partial_{\mu} \phi \right)} \partial_{\mu} \left( \epsilon^{a} G_{a} \left( \phi \right) \right) \right] \\
&=& \epsilon^{a} \int d^{d} x \left[ \frac{\partial \mathcal{L}}{\partial \phi} G_{a} \left( \phi \right) – \partial_{\mu} \left( \frac{\partial \mathcal{L}}{\partial \left( \partial_{\mu} \phi \right)} \right) G_{a} \left( \phi \right) + \partial_{\mu} \left( \frac{\partial \mathcal{L}}{\partial \left( \partial_{\mu} \phi \right)} G_{a} \left( \phi \right) \right) \right] \tag{5} \label{dac2}
\end{eqnarray}
と変化します。
式 \eqref{dac2} の最右辺の第1項と第2項は、オイラー・ラグランジュ方程式(式 \eqref{eleq})からゼロになり
\begin{eqnarray}
\delta S = \epsilon^{a} \int d^{d} x \partial_{\mu} \left( \frac{\partial \mathcal{L}}{\partial \left( \partial_{\mu} \phi \right)} G_{a} \left( \phi \right) \right) \tag{6} \label{dac3}
\end{eqnarray}
と言う形になります。
この時に \( \delta S = 0 \) つまり
\begin{eqnarray}
\partial_{\mu} \left( \frac{\partial \mathcal{L}}{\partial \left( \partial_{\mu} \phi \right)} G_{a} \left( \phi \right) \right) = 0 \tag{7} \label{dac4}
\end{eqnarray}
となる必要があります。
ここで
\begin{eqnarray}
j_{a}^{\mu} \equiv \frac{\partial \mathcal{L}}{\partial \left( \partial_{\mu} \phi \right)} G_{a} \left( \phi \right) \tag{8} \label{nc}
\end{eqnarray}
とおくと \( \partial_{\mu} j_{a}^{\mu} = 0 \) なり、 これはカレントが保存される事を意味しています。
このように、式 \eqref{dac4} を満たすカレント \( j_{a}^{\mu} \) をネーターカレントと言います。
また、ネーターカレントの時間成分を全空間で積分した量(チャージ)を
\begin{eqnarray}
Q_{a} \equiv \int d^{d-1} x j_{a}^{0} \tag{9} \label{charge}
\end{eqnarray}
と定義します。
このチャージは
\begin{eqnarray}
\frac{dQ_{a}}{dt} = \int d^{d-1} x \partial_{0} j_{a}^{0} = – \int d^{d-1} x \partial_{i} j_{a}^{I} = 0 \tag{10} \label{charge2}
\end{eqnarray}
を満たしており、保存量であることが分かります。
なお式 \eqref{charge2} 内の \( – \int d^{d-1} x \partial_{i} j_{a}^{I} = 0 \) は、ガウスの発散の定理と無限遠の表面項を無視する境界条件を利用しました。
以上のように『系が連続変換(式 \eqref{inftra})に対して連続対称性があるならば、保存量 \( Q_{a} \) が存在する』と言うネーターの定理が示されました。
エネルギー運動量テンソル
ネーターの定理は任意の連続変換に対して成り立ちますが、以下では重要な具体例の一つである
『並進対称性』およびそれに対応する保存則を説明します。
座標系を取り直し、無限小並進を
\begin{eqnarray}
x^{\mu} \rightarrow x^{\prime \mu} = x^{\mu} – \epsilon^{\mu} \tag{11} \label{xtra}
\end{eqnarray}
とします。
新しい座標 \( x^{\prime} \) でのスカラー場を \( \phi^{\prime}(x^{\prime}) = \phi(x) \) で定義すると、位置 \( x \) での値は
\begin{eqnarray}
\phi (x) \rightarrow \phi^{\prime}(x) &=& \phi^{\prime} (x^{\prime} + \epsilon) = \phi (x + \epsilon) \\
&=& \phi (x) + \epsilon^{\mu} \partial_{\mu} \phi (x) \tag{12} \label{ptrat}
\end{eqnarray}
と変化します。
またラグランジアン密度もスカラー量であるため
\begin{eqnarray}
\mathcal{L} \rightarrow \mathcal{L}^{\prime} &=& \mathcal{L} + \epsilon^{\mu} \partial_{\mu} \mathcal{L} \\
&=& \mathcal{L} + \epsilon^{\mu} \partial_{\mu} \left( \delta^{\mu}_{\nu} \mathcal{L} \right) \tag{13} \label{ltrat}
\end{eqnarray}
のように変換されます。
したがって、系に連続並進対称性がある場合のネーターカレントは
\begin{eqnarray}
T^{\mu}_{\nu} = \frac{\partial \mathcal{L}}{\partial \left( \partial_{\mu} \phi \right)} \partial_{\nu} \phi – \delta^{\mu}_{\nu} \mathcal{L} \tag{14} \label{emt}
\end{eqnarray}
となります。
式 \eqref{emt} で定義されるネーターカレントを特に「エネルギー運動量テンソル」と言います。
対応する保存量(チャージ)は
\begin{eqnarray}
H \equiv \int d^{d-1} x T^{0}_{0}
P^{j} \equiv \int d^{d-1} x T^{0}_{j}
\end{eqnarray}
となり、ハミルトニアン \( H \) や運動量 \( P^{j} \) を与えます。
まとめ
場の量子論の前段階および場の解析力学の導入として「ネーターの定理」について解説しました。
本記事をサクッと読んだ上で、以下に示す参考書籍を基にして、手を動かしてより詳細な議論を行なってみて下さい。
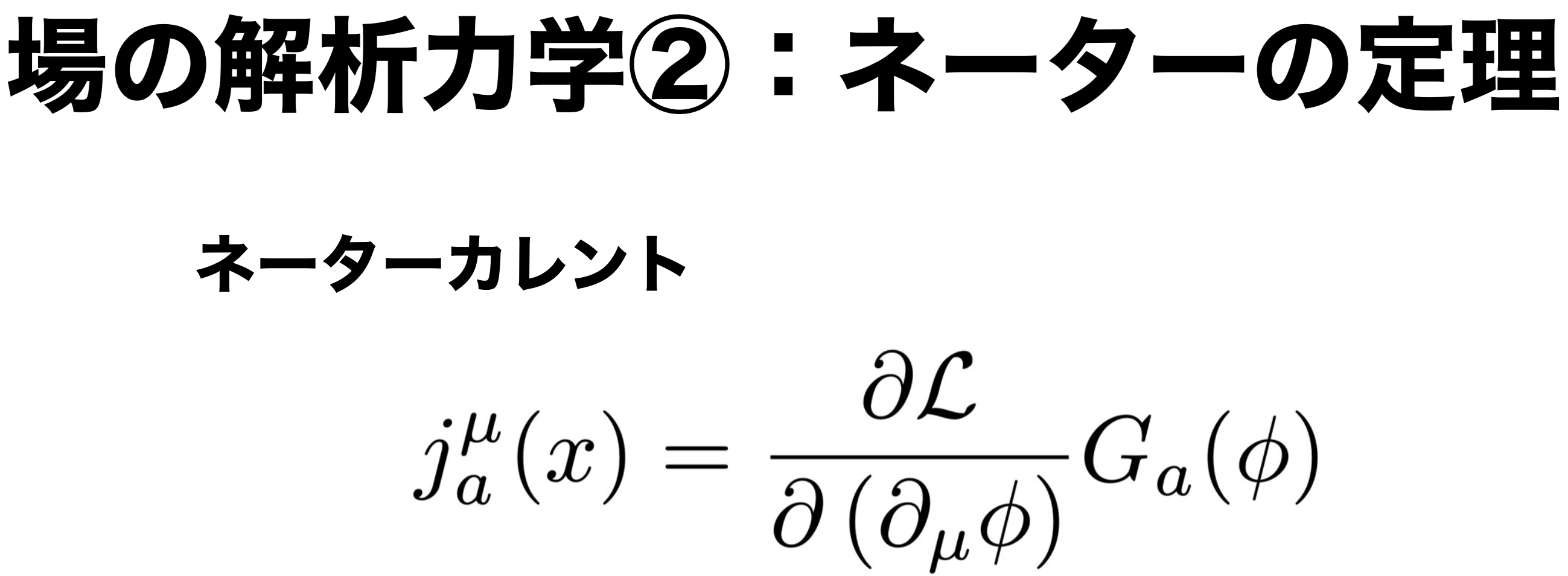

コメント