- 量子力学を既習であり、経路積分を自習したい学部生(学部3〜4年前期程度)
- 場の量子論の入門として経路積分を学びたい大学院生(修士課程程度)
この記事では、場の量子論の入門として「相関関数の経路積分表示」をご紹介します。
本記事を読むことで
経路積分量子化の手順で、「\( n \) 点相関関数」を計算する感覚を掴んで頂けると幸いでございます。
本記事を執筆している、私トーマは、物理学者として勤務しています。
そんな私が分かりやすく解説いたします。
導入・計算の準備
量子力学などで、系の状態を議論する上で重要な物理量に「相関関数」があります。
物理量演算子 \( \hat{A}, \hat{B} \) の相関関数は
\begin{eqnarray}
\left \langle \hat{A} \hat{B} \right \rangle \tag{1} \label{ab}
\end{eqnarray}
のように、\( \hat{A} \) と \( \hat{B} \) の積の平均として表されます。
本記事では、1自由度の量子力学から、相関関数の計算の導入を行います。
遷移確率の復習
私が以前書いた記事
の内容を、大雑把に結果だけを羅列したいと思います。
計算過程は、上記の記事を参考にしてください。
時刻 \( t_{i} \) に位置 \( x_{i} \) にあった粒子が、時刻 \( t_{f} \) に位置 \( x_{f} \) に遷移する確率は
\begin{align}
& \left \langle q_{f} ,t_{f} \right. \left| q_{i}, t_{i} \right \rangle \notag \\
& \hspace{1em} = \int [ dp dq ] \exp \left[ i \int_{t_{i}}^{t_{f}} dt \left( p \dot{q} -H (p,q) \right) \right] \tag{2} \label{protralim}
\end{align}
と書けます。
ここで \( \left[ dp dq \right] \) は経路積分の測度です。
ハミルトニアン演算子を
\begin{eqnarray}
\hat{H}(\hat{p}, \hat{q}) = \frac{1}{2} \hat{p}^{2} + V \left( \hat{q} \right) \tag{3} \label{hampq}
\end{eqnarray}
とすると、式 \eqref{protralim} で \( p \) に関するガウス積分を実行して
\begin{eqnarray}
&& \left \langle q_{f} ,t_{f} \right. \left| q_{i}, t_{i} \right \rangle \notag \\
&& \hspace{1em} = \int [ dq ] \exp \left[ i \int_{t_{i}}^{t_{f}} dt \left( \frac{1}{2} \dot{q}^{2} – V(q) \right) \right] \notag \\
&& \hspace{1em} = \int [ dq ] \exp \left[ i \int_{t_{i}}^{t_{f}} dt L \left( q, \dot{q} \right) \right] \\
&& \hspace{1em} = \int [ dq ] \exp \left( i S \right) \tag{4} \label{prolag}
\end{eqnarray}
得ます。
ただしここで、\( L \left( q, \dot{q} \right) \) はラグランジアンであり、作用 \( S \) を
\begin{eqnarray}
S \equiv \int_{t_{i}}^{t_{f}} dt L \left( q, \dot{q} \right) \tag{5} \label{actions}
\end{eqnarray}
と定義しました。
\( n \) 点相関関数の計算
ある時刻 \( t_{i} < t < t_{f} \) に \( q(t) \) を挿入した経路積分
\begin{eqnarray}
&& \int [dq] q(t) \exp \left[ i \int_{t_{i}}^{t_{f}} dt L \left( q, \dot{q} \right) \right] \notag \\
&& \hspace{3em} = \int dq \int [dq]^{\prime} \exp \left[ i \int_{t}^{t_{f}} dt L \left( q, \dot{q} \right) \right] q \exp \left[ i \int_{t_{t}}^{t} dt L \left( q, \dot{q} \right) \right] \tag{6} \label{patht}
\end{eqnarray}
のように書き表せます。
ただし \( [dq]^{\prime} \) は時刻 \( t \) での \( q \) 積分を除いた経路積分の測度を意味しています。
この表式は
\begin{eqnarray}
\int dq \left \langle q_{f} ,t_{f} \right. \left| q, t \right \rangle q \left \langle q, t \right. \left| q_{i}, t_{i} \right \rangle &=& \int dq \left \langle q_{f} ,t_{f} \right| \hat{q}(t) \left| q, t \right \rangle \left \langle q, t \right. \left| q_{i}, t_{i} \right \rangle \notag \\
&=& \left \langle q_{f} ,t_{f} \right| \hat{q}(t) \left| q_{i}, t_{i} \right \rangle \tag{7} \label{patht2}
\end{eqnarray}
のように書き換えられます。
つまり、演算子 \( \hat{q}(t) \) の挿入と等価であることがわかります。
同様に、時刻 \( t_{i} < t, t^{\prime} < t_{f} \) に関して、積 \( q(t)q(t^{\prime}) \) を経路積分に挿入してみます。
演算子に置き換えると、時間順序に並ぶことから
\begin{eqnarray}
\int [dq] q(t)q(t^{\prime}) \exp \left[ i \int_{t_{i}}^{t_{f}} dt L \left( q, \dot{q} \right) \right] = \left \langle q_{f} ,t_{f} \right| T \left[ \hat{q}(t) \hat{q}(t^{\prime}) \right] \left| q_{i}, t_{i} \right \rangle \tag{8} \label{pathtt}
\end{eqnarray}
が得られます。
ここで、時間順序積
\begin{eqnarray}
T \left[ \hat{A}(t) \hat{B}(t^{\prime}) \right] = \left \{
\begin{array}{ll}
\hat{A}(t) \hat{B}(t^{\prime}) & (t > t^{\prime}) \\
\hat{B}(t^{\prime}) \hat{A}(t) & (t^{\prime} > t)
\end{array}
\right. \tag{9} \label{torder}
\end{eqnarray}
を導入しました。
同様に、一般の積 \( q(t_{1}) \cdots q(t_{n}) \) の挿入も、演算子の時間順序積の挿入に対応することがわかります。
\begin{eqnarray}
&& \int [dq] q(t_{1}) \cdots q(t_{n}) \exp \left[ i \int_{t_{i}}^{t_{f}} dt L \left( q, \dot{q} \right) \right] \notag \\
&& \hspace{3em} = \left \langle q_{f} ,t_{f} \right| T \left[ \hat{q}(t_{1}) \cdots \hat{q}(t_{n}) \right] \left| q_{i}, t_{i} \right \rangle \tag{10} \label{pathtn}
\end{eqnarray}
ユークリッド化した時間 \( \tau \)における相関関数
次に \( t \rightarrow \tau = it \) と、時間をユークリッド化した場合を考えます。
ここで、エネルギー固有状態を
\begin{eqnarray}
\hat{H} \left| n \right \rangle = E_{n} \left| n \right \rangle \tag{11} \label{heigen}
\end{eqnarray}
とし、その完全系 \( \displaystyle{\sum_{n}} \left| n \right \rangle \left \langle n \right| = 1 \) を挿入することで、遷移確率を
\begin{eqnarray}
\left \langle q_{f} ,t_{f} \right. \left| q, t \right \rangle &=& \left \langle q_{f} \right| \exp \left[ -i \hat{H} t_{f} \right] \left| q, t \right \rangle \notag \\
&=& \sum_{n} \left \langle q_{f} \right. \left| n \right \rangle \exp \left[ -i E_{n} t_{f} \right] \left \langle n \right. \left| q, t \right \rangle \tag{12} \label{protran}
\end{eqnarray}
と書き直すことが出来ます。
ここで \( t_{f} \rightarrow \tau_{f} = it_{f} \) とし \( \tau_{f} \rightarrow \infty \) の極限を取るとエネルギーの最も低い基底状態 \( \left| 0 \right \rangle \) のみの寄与が残ります。
したがって \( \tau_{f} \rightarrow \infty \) の極限で
\begin{eqnarray}
\left \langle q_{f} ,t_{f} \right. \left| q, t \right \rangle \rightarrow \exp \left( – E_{0} \tau_{f} \right) \left \langle q_{f} \right. \left| 0 \right \rangle \left \langle 0 \right. \left| q, t \right \rangle \tag{13} \label{protran2}
\end{eqnarray}
となります。
表式 \eqref{pathtn} を拡張し \( \tau_{f} \rightarrow \infty \), \( \tau_{i} \rightarrow -\infty \) とすると
\begin{eqnarray}
&& \left \langle q_{f} ,t_{f} \right| T \left[ \hat{q}(t_{1}) \cdots \hat{q}(t_{n}) \right] \left| q_{i}, t_{i} \right \rangle \notag \\
&& \hspace{1em} \rightarrow \exp \left[ -E_{0} \left( \tau_{f} – \tau_{i} \right) \right] \int dqdq^{\prime} \left \langle q_{f} \right. \left| 0 \right \rangle \left \langle 0 \right. \left| q, t \right \rangle \notag \\
&& \hspace{6em} \times \left \langle q, t \right| T \left[ \hat{q}(t_{1}) \cdots \hat{q}(t_{n}) \right] \left| q^{\prime}, t^{\prime} \right \rangle \left \langle q^{\prime}, t^{\prime} \right. \left| 0 \right \rangle \left \langle 0 \right. \left| q_{i} \right \rangle \notag \\
&& \hspace{1em} = \exp \left[ -E_{0} \left( \tau_{f} – \tau_{i} \right) \right] \left \langle q_{f} \right. \left| 0 \right \rangle \left \langle 0 \right| T \left[ \hat{q}(t_{1}) \cdots \hat{q}(t_{n}) \right] \left| 0 \right \rangle \left \langle 0 \right. \left| q_{i} \right \rangle \tag{14} \label{pathtn2}
\end{eqnarray}
となります。
この表式から \( n \) 点相関関数は、経路積分の言葉から
\begin{eqnarray}
&& \left \langle 0 \right| T \left[ \hat{q}(t_{1}) \cdots \hat{q}(t_{n}) \right] \left| 0 \right \rangle \notag \\
&& \hspace{1em} = \lim_{\tau_{i} \rightarrow -\infty, \, \tau_{f} \rightarrow \infty} \left[ \frac{\left \langle q_{f} ,t_{f} \right| T \left[ \hat{q}(t_{1}) \cdots \hat{q}(t_{n}) \right] \left| q_{i}, t_{i} \right \rangle}{\left \langle q_{f}, t_{f} \right. \left| q_{i}, t_{i} \right \rangle} \right] \notag \\
&& \hspace{1em} = \frac{\int [dq] q(t_{1}) \cdots q(t_{n}) \exp [-S_{\mathrm{E}} (q, \dot{q})]}{\int [dq] \exp [-S_{\mathrm{E}} (q, \dot{q})]} \tag{15} \label{corre}
\end{eqnarray}
のように表せます。
ここで、ユークリッド化した作用とラグランジアンを
\begin{eqnarray}
S_{\mathrm{E}} = \int d \tau L_{\mathrm{E}} (q, \partial_{\tau} q) = – \int d \tau L_{\mathrm{E}} (q, i \partial_{\tau} q) \tag{16} \label{euac}
\end{eqnarray}
で定義しました。
まとめ
1自由度の量子力学の経路積分量子化の手順で
「相関関数」の計算をまとめました。
本記事をサクッと読んだ上で、以下に示す参考書籍を基にして、手を動かしてより詳細な議論を行なってみて下さい。
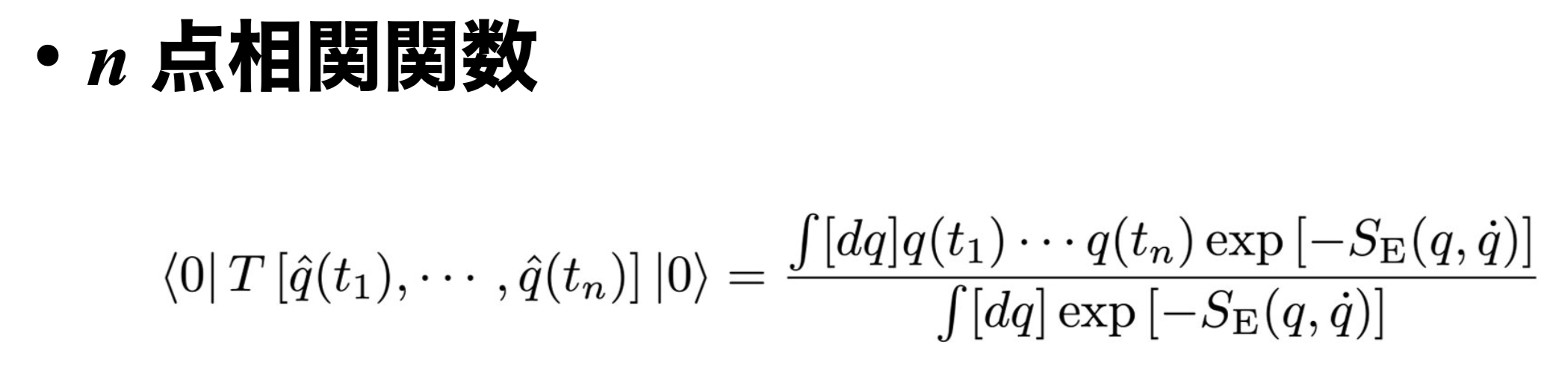


コメント