【Pythonで学ぶ】数値積分入門：合成中点則

数値計算なんて一度も学んだことがない or 学んだことがあるけど入門レベルから勉強し直したい
でも本や教科書には、解説は載っているけどソースコードが載っていないことが多くて困る
Pythonで手を動かしながら、数値計算の初歩を学びたい

こういった悩みを抱えた読者さんを想定しています。

この記事では、数値計算や計算物理の初歩である「数値積分：合成中点則」の導入的知識とプログラミングについて、Python言語を用いて説明します。

本記事を読み終える頃には
初学者の方でも、Pythonで手を動かして例題を解くことで、数値積分のコツを掴めるようになります。

本記事を執筆している、私トーマは、東京大学で物理学者として勤務し、理論物理や数値計算プログラミングに関する仕事をしています

数値積分の基本
1. 中点則
2. 合成中点則
実際に問題を解いてみよう
1. 考え方
2. 解答・ソースコード
もっと学びたい方へ
まとめ
参考書籍

数値積分の基本

Pythonでは、scipy.integrate モジュールを用いることで大抵の積分処理を行うことができます。
ここに実装されている関数には、計算の高速化や安定性向上のための様々な工夫が施されています。

しかし本記事では、そのようなアルゴリズムの詳細には立ち入らず、むしろもっと基本的な考え方やその利用方法に絞って解説していきます。

ある関数 \( f(x) \) を区間 \( [a,b] \) で積分すること、つまり
\begin{eqnarray}
I = \int_{a}^{b} f(x) dx \tag{1} \label{int}
\end{eqnarray}
を考えます。

数値計算では連続的な変数 \( x \) を扱うことができないため、適当に離散化して有限要素の輪として積分を評価します。

中点則

まず、最も大雑把な評価として、積分を一点で近似することを考えます。
つまり
\begin{eqnarray}
I \approx S = h f(x_{0}) \tag{2} \label{approx}
\end{eqnarray}
と近似します。
ただしここで、 \( x_{0} = \displaystyle{\frac{a+b}{2}} \), \( h = b – a \) とします。

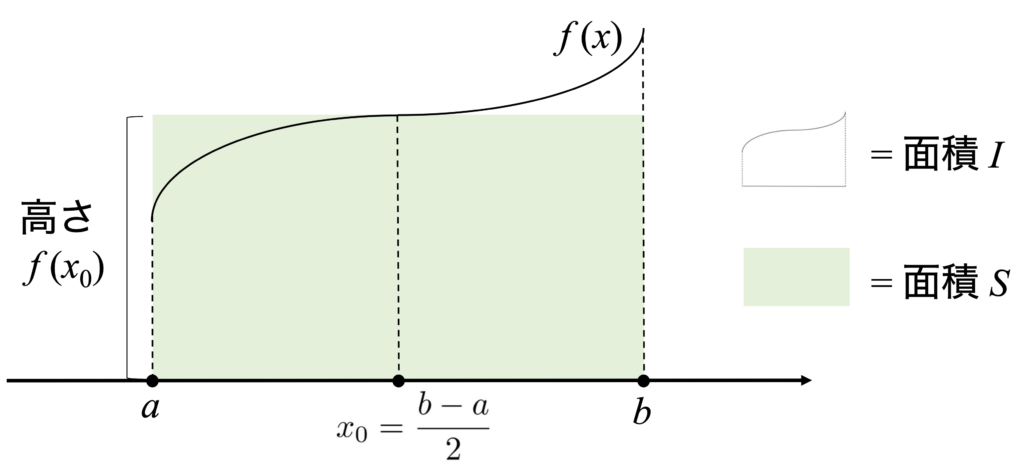
これは、積分 \( I \) で表されるグラフの面積を、縦 \( f(x_{0}) \) 横 \( h \) の長方形の面積で近似するという、だいぶ大雑把な評価であることが分かります。
（下図参照）

この近似による誤差を評価するために、式 \eqref{int} を \( x_{0} \) 周りでテイラー級数展開すると
\begin{eqnarray}
I &=& \sum_{n=0}^{\infty} \frac{f^{(n)}(x_{0})}{n !} \int_{a}^{b} (x-x_{0})^{n} dx \notag \\
&=& h f(x_{0}) + \frac{h^{3}}{24} f^{(2)}(x_{0}) + \frac{h^{5}}{1920} f^{(4)}(x_{0}) + O \left( h^{7} \right) \tag{3} \label{taylor}
\end{eqnarray}
と書けます。

したがって、近似 \( S \) の誤差 \( \epsilon \) は
\begin{eqnarray}
\epsilon = \left| I – S \right| = O \left( h^{3} \right) \tag{4} \label{error}
\end{eqnarray}
であることが分かります。
これは「中点則」と呼ばれる評価方法で、\( h \) が（\( f(x) \) の変化量に対して）十分小さければ、それなりに良い近似になります。

逆に言うと \( h \) が大きい場合には、良い近似にはなり得ません。
この場合はどうしたら良いのでしょうか？

\( h \) が大きい場合の単純な解決策として
合成中点則という手法を、以下の節で解説します。

合成中点則

合成中点則では
区間 \( [a,b] \) を \( n \) 個の微小区間 \( i \in \{ 0, \cdots, n-1 \} \) に分割し、それぞれの区間に中点則を適用します。
※ Python のインデックスは 0 から始まるため、微小区間のラベルもその表式に合わせました。

この時、積分 \( I \) は以下のように変形できます
\begin{eqnarray}
I = \sum_{i=0}^{n-1} \int_{a+\frac{h}{n}i}^{a+\frac{h}{n}(i+1)} f(x) dx \tag{5} \label{int2}
\end{eqnarray}

それぞれの微小区間の中点は \( x_{i} = a + h \displaystyle{\frac{2i + 1}{2n}} \) で与えられます。
各区間に中点則を適用したのち、全ての寄与を足し合わせることで
\begin{eqnarray}
S = \frac{h}{n} \sum_{i=0}^{n-1} f(x_{i}) \tag{6} \label{approx2}
\end{eqnarray}
が得られます。

分割数 \( n \) が大きいほど精度が良くなると期待されます。
各区間における \( f(x) \) を \( x_{i} \) 周りでテイラー級数展開して評価すると誤差 \( \epsilon \) は
\begin{eqnarray}
\epsilon = O \left( \frac{h^{3} \langle f^{(2)} \rangle}{n^{2}} \right) \tag{7} \label{error2}
\end{eqnarray}
となります。
ただし \( \langle f^{(2)} \rangle = \displaystyle{\frac{1}{n} \sum_{i=0}^{n-1} f^{(2)}(x_{i})} \) としました。

実際に問題を解いてみよう

問題

合成中点則を実装して、積分
\begin{eqnarray}
\int_{0}^{1}dx \, e^{-x} \tag{}
\end{eqnarray}
を実行せよ。
また、刻み幅を変えて、精度と計算時間の変化を確認せよ。

考え方

式 \eqref{approx2} を実装します。
被積分関数部分と積分部分とを分けて関数にしておくと、後で別の関数を積分したい場合に再利用できて便利です。

解答・ソースコード

被積分関数部分を以下のように定義します。

import numpy as np

def func(x):
    return np.exp(-x)   # 指数関数はnumpyのものを用いる

積分部分に関しては、例えば式 \eqref{approx2} の \( x_{i} \)、 \( h \) などの変数を用いて、以下のように定義します。

def midpoint(func, a, b, n):
    h, ans = (b-a)/n, 0    # hの定義が本文と1/n倍異なる点に注意
    for i in range(n):
        xi = a + h*(2*i+1)/2
        ans = ans + func(xi)*h
    return ans

これを用いて誤差評価をします。
例えば、解析解 \( 1-e^{-1} \) を用いて、以下のように書きます。

from time import time
I = 1 - np.exp(-1)
for n in [10**i for i in range(0,7,2)]:
    # n=10^0, 10^2, 10^4, 10^6で評価する
    t = time()
    S = midpoint(func, 0, 1, n)
    error = abs((S-I)/S)    # ここでは相対誤差を用いている
    txt = "n={0:.0e} t={1:.2e}s, S={2:.2e}, e={3:.3e}"\
            .format(n, time()-t, S, error)
    # eは指数表記の指定、.xで小数点以下の桁数(x)を指定する
    print(txt)

以上のコードを実行してみましょう。
分割数 \( n \) が大きくなるほど、誤差が小さくなることを確認できるはずです。