- 量子力学を既習であり、経路積分を自習したい学部生(学部3〜4年前期程度)
- 場の量子論の入門として経路積分を学びたい大学院生(修士課程程度)
この記事では、場の量子論の入門として「相関関数の経路積分表示」をご紹介します。
本記事を読むことで
経路積分量子化の手順で、重要な物理量の一つである「遷移確率」を計算する感覚を掴んで頂けると幸いでございます。
本記事を執筆している、私トーマは、物理学者として勤務しています。
そんな私が分かりやすく解説いたします。
導入・計算の準備
演算子の時間依存性
量子力学では、座標演算子 \( \hat{q} \) と共役運動量演算子 \( \hat{p} \) とを基本要素としています。
これらの演算子は交換関係
\begin{eqnarray}
\left[ \hat{q}, \hat{p} \right] = i \hbar \tag{1} \label{comu}
\end{eqnarray}
を満たします。
なお以下では、ディラック定数が \( \hbar = 1 \) となるような単位系を扱うこととします。
系のハミルトニアン演算子 \( \hat{H} \left( \hat{p}, \hat{q} \right) \) はこれらに依存する関数であるとします。
ハイゼンベルグ描像により、座標および共役運動量演算子の時間依存性は
\begin{eqnarray}
\hat{q}(t) &=& \exp \left( i \hat{H} t \right) \hat{q} \exp \left( -i \hat{H} t \right) \tag{2} \label{qt} \\
\hat{p}(t) &=& \exp \left( i \hat{H} t \right) \hat{p} \exp \left( -i \hat{H} t \right) \tag{3} \label{pt}
\end{eqnarray}
と書きます。
例えば、時間に依存する座標演算子の固有状態を
\begin{eqnarray}
\hat{q}(t) \left| q, t \right \rangle = q \left| q, t \right \rangle \tag{4} \label{eigens}
\end{eqnarray}
のように導入します。
この固有状態は、シュレディンガー描像の固有状態 \( \left| q \right \rangle \) と
\begin{eqnarray}
\left| q, t \right \rangle = \exp \left( i \hat{H} t \right) \left| q \right \rangle \tag{5} \label{shhei}
\end{eqnarray}
という関係にあります。
共役運動量演算子の固有状態 \( \left| p, t \right \rangle \) および \( \left| p \right \rangle \) に関しても、式 \eqref{eigens} & \eqref{shhei} と同様に書けます。
固有状態の内積等
シュレディンガー描像の、位置と共役運動量に関する固有状態 \( \left| q \right \rangle \) および \( \left| p \right \rangle \) に関しての内積 \( \left \langle q \right. \left| p \right \rangle \) を計算します。
まず内積 \( \left \langle q \right. \left| q^{\prime} \right \rangle \) に、運動量に関する完全系 \( \displaystyle{\int dp \left| p \right \rangle \left \langle p \right| } = 1 \) を代入すると
\begin{eqnarray}
\left \langle q \right. \left| q^{\prime} \right \rangle = \int dp \left \langle q \right. \left| p \right \rangle \left \langle p \right. \left| q^{\prime} \right \rangle \tag{6} \label{kanzen}
\end{eqnarray}
となります。
また \( \left \langle q \right. \left| q^{\prime} \right \rangle = \delta(q-q^{\prime}) \) なので、フーリエ変換を用いると
\begin{eqnarray}
\left \langle q \right. \left| q^{\prime} \right \rangle &=& \delta(q-q^{\prime}) \notag \\
&=& \int \frac{dp}{2\pi} \exp \left[ i p \left( q – q^{\prime} \right) \right] \tag{7} \label{fou}
\end{eqnarray}
となります。
以上のことから、式 \eqref{kanzen} と式 \eqref{fou} を比較することで
\begin{eqnarray}
\left \langle q \right. \left| p \right \rangle = \frac{1}{\sqrt{2\pi}} \exp(iqp) \tag{8} \label{inner}
\end{eqnarray}
を得ました。
遷移確率の計算
量子力学における重要な物理量として「遷移確率」があります。
時刻 \( t_{i} \) に位置 \( x_{i} \) にあった粒子が、時刻 \( t_{f} \) に位置 \( x_{f} \) に遷移する確率は
\begin{eqnarray}
\left \langle q_{f} ,t_{f} \right. \left| q_{i}, t_{i} \right \rangle = \left \langle q_{f} \right| \exp \left[ i \hat{H} (t_{f} – t_{i}) \right] \left| q_{i} \right \rangle \tag{9} \label{protra}
\end{eqnarray}
で与えられます。
ここで、時間間隔を \( N \) 等分し
\begin{eqnarray}
t_{m} = t_{i} + m\epsilon, \hspace{1em} \epsilon = \frac{t_{f} – t_{i}}{N}, \hspace{1em} m = 0, \cdots, N \tag{10} \label{timen}
\end{eqnarray}
と定義します。
\( t_{0} = t_{I} \)、\( t_{N} = t_{f} \) となります。
さらに、時刻 \( t_{m} \) における完全系 \( \displaystyle{\int dq_{m} \left| q_{m}, t_{m} \right \rangle \left \langle q_{m} ,t_{m} \right| } = 1 \) を式 \eqref{protra} に代入すると、遷移確率は以下のように式変形できます。
\begin{eqnarray}
&& \left \langle q_{f} ,t_{f} \right. \left| q_{i}, t_{i} \right \rangle \notag \\
&& \hspace{1em} = \left \langle q_{f} ,t_{f} \right| \left( \int dq_{N-1} \left| q_{N-1}, t_{N-1} \right \rangle \left \langle q_{N-1} ,t_{N-1} \right| \right) \notag \\
&& \hspace{7em} \times \cdots \times \left( \int dq_{1} \left| q_{1}, t_{1} \right \rangle \left \langle q_{1} ,t_{1} \right| \right) \left| q_{i}, t_{i} \right \rangle \notag \\
&& \hspace{1em}= \int dq_{N-1} \cdots dq_{1} \left \langle q_{N} ,t_{N} \right. \left| q_{N-1}, t_{N-1} \right \rangle \cdots \left \langle q_{1} ,t_{1} \right. \left| q_{0}, t_{0} \right \rangle \tag{11} \label{protra2}
\end{eqnarray}
と表すことが出来ます。
時刻 \( t_{m} \) での要素
式 \eqref{protra2}より、時刻 \( t_{m} \) での遷移確率の要素は
\begin{eqnarray}
\left \langle q_{m+1} ,t_{m+1} \right. \left| q_{m}, t_{m} \right \rangle = \left \langle q_{m+1} \right| \exp \left( -i \hat{H} \epsilon \right) \left| q_{m} \right \rangle \tag{12} \label{protram}
\end{eqnarray}
と書けます。
式 \eqref{protram} に、共役運動量に関する完全系 \( \displaystyle{\int d p_{m} \left| p_{m} \right \rangle \left \langle q_{m} \right| } = 1 \) を代入すると
\begin{eqnarray}
\left \langle q_{m+1} ,t_{m+1} \right. \left| q_{m}, t_{m} \right \rangle = \int dp_{m} \left \langle q_{m+1} \right. \left| p_{m} \right \rangle \left \langle p_{m} \right| \exp \left( -i \hat{H} \epsilon \right) \left| q_{m} \right \rangle \tag{13} \label{protram2}
\end{eqnarray}
となります。
ここで、\( i \hat{H} \epsilon = 0 \) 近傍でのテイラー級数展開
\begin{eqnarray}
\exp \left( i \hat{H} \epsilon \right) = \sum_{j=0}^{\infty} \frac{\left( i \epsilon \right)^{j}}{j!} \left[ \hat{H} \left( \hat{p}, \hat{q} \right) \right]^{j} \tag{14} \label{taylore}
\end{eqnarray}
を考え、かつ
\begin{eqnarray}
\left \langle p_{m} \right| \hat{H} \left( \hat{p}, \hat{q} \right) \left| q_{m} \right \rangle = H \left( p_{m}, q_{m} \right) \left \langle p_{m} \right. \left| q_{m} \right \rangle \tag{15} \label{eigenh}
\end{eqnarray}
なので、式 \eqref{inner} を利用すると
\begin{eqnarray}
&& \left \langle q_{m+1} ,t_{m+1} \right. \left| q_{m}, t_{m} \right \rangle \notag \\
&& \hspace{1em} = \int dp_{m} \exp \left[ -i H \left( p_{m}, q_{m} \right) \epsilon \right] \left \langle q_{m+1} \right. \left| p_{m} \right \rangle \left \langle p_{m} \right. \left| q_{m} \right \rangle \notag \\
&& \hspace{1em} = \int \frac{dp_{m}}{2\pi} \exp \left[ ip_{m} \left( q_{m+1} – q_{m} \right) – i H \left( p_{m}, q_{m} \right) \epsilon \right] \tag{16} \label{protram3}
\end{eqnarray}
を得ます。
\( N \rightarrow \infty \) の極限
式 \eqref{protram3} を式 \eqref{protra2} をに代入すると
\begin{eqnarray}
&& \left \langle q_{f} ,t_{f} \right. \left| q_{i}, t_{i} \right \rangle \notag \\
&& \hspace{1em} = \lim_{N \rightarrow \infty} \int \left[ \prod_{m=1}^{N-1} \frac{dp_{m} dq_{m}}{2\pi} \right] \frac{dp_{0}}{2\pi} \exp \left[ i \sum_{m=0}^{N-1} \left[ p_{m} \left( q_{m+1} – q_{m} \right) – H \left( p_{m}, q_{m} \right) \epsilon \right] \right] \\
&& \hspace{1em} \equiv \int [ dp dq ] \exp \left[ i \int_{t_{i}}^{t_{f}} dt \left( p \dot{q} -H (p,q) \right) \right] \tag{17} \label{protralim}
\end{eqnarray}
と書けます。
ここで、離散変数 \( (p_{m}, q_{m}) \) が連続変数 \( (p, q) \) になり、 \( \left[ dp dq \right] \) で経路積分の測度を表しています。
ラグランジアンの導入
ここでハミルトニアン演算子が
\begin{eqnarray}
\hat{H}(\hat{p}, \hat{q}) = \frac{1}{2} \hat{p}^{2} + V \left( \hat{q} \right) \tag{18} \label{hampq}
\end{eqnarray}
と書けるとすると、式 \eqref{protralim} で \( p \) に関するガウス積分を実行して
\begin{eqnarray}
&& \left \langle q_{f} ,t_{f} \right. \left| q_{i}, t_{i} \right \rangle \notag \\
&& \hspace{1em} = \int [ dq ] \exp \left[ i \int_{t_{i}}^{t_{f}} dt \left( \frac{1}{2} \dot{q}^{2} – V(q) \right) \right] \notag \\
&& \hspace{1em} \equiv \int [ dq ] \exp \left[ i \int_{t_{i}}^{t_{f}} dt L \left( q, \dot{q} \right) \right] \tag{19} \label{prolag}
\end{eqnarray}
と書けます。
ただしここで、\( L \left( q, \dot{q} \right) \) はラグランジアンです。
ここで作用 \( S \) を
\begin{eqnarray}
S \equiv \int_{t_{i}}^{t_{f}} dt L \left( q, \dot{q} \right) \tag{20} \label{actions}
\end{eqnarray}
と定義すると、遷移確率は\( \exp(iS) \) の \( q \) 積分の形で表すことが出来ます。
まとめ
1自由度の量子力学の経路積分量子化の手順で
「遷移確率」の計算をまとめました。
本記事をサクッと読んだ上で、以下に示す参考書籍を基にして、手を動かしてより詳細な議論を行なってみて下さい。
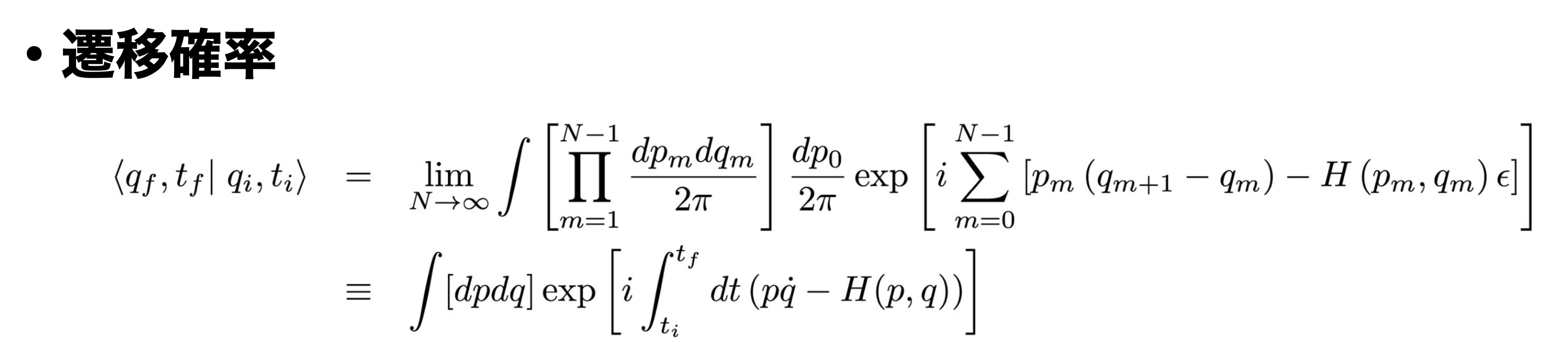


コメント